Μηχανική Ενέργεια (Υποθέτουμε ότι δεν υπάρχουν Τριβές)
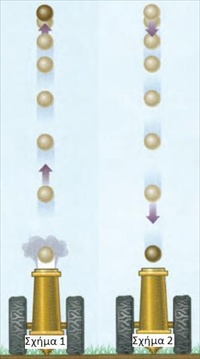
Στο Σχήμα 1, η Ε
του βλήματος μετατρέπεται σταδιακά σε Ε
.
Η κινητική ενέργεια μηδενίζεται στο μέγιστο ύψος.
Στο Σχήμα 2, η Ε
του βλήματος μετατρέπεται σε Ε
κατά την πτώση του.
Σε οποιοδήποτε σημείο μεταξύ των θέσεων (Α) και (Δ) κατά την άνοδο ή την κάθοδό του βλήματος, το άθροισμα των ενεργειών:
Ε
κινητική + Ε
δυναμική παραμένει
και ονομάζεται
Ενέργεια (Ε
μηχανική)
Άσκηση:
Στο επόμενο Σχήμα, δίνονται: μάζα αθλητή m=50Kg, επιτάχυνση της βαρύτητας g=10m/s
2, μέγιστο ύψος h=5m, αρχική ταχύτητα αθλητή v
α=0 m/s και ΔΕΝ υπάρχουν τριβές.
Σαν επίπεδο αναφοράς δυναμικής ενέργειας (h=0m) επιλέγουμε το κατώτατο σημείο της τροχιάς του αναβάτη.
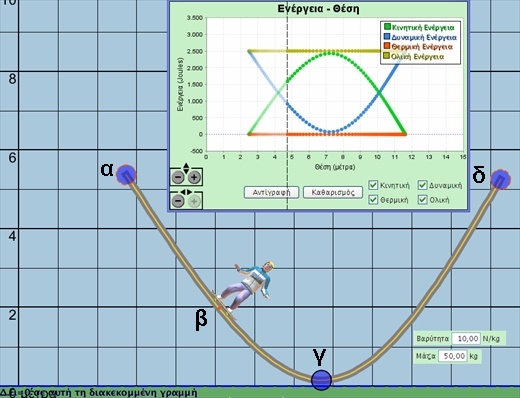
Α1) Υπολογίστε τη δυναμική ενέργεια του αθλητή στο σημείο α.
Ε
δυναμική α =
* h =>
Ε
δυναμική α = m * g * h =>
Ε
δυναμική α = 50
* 10
/
2 * 5
=>
Ε
δυναμική α =
Joule.
Α2) Υπολογίστε την κινητική ενέργεια του αθλητή στο σημείο α.
Ε
κινητική α = 0,5 * μάζα m * ταχύτητα v
2 =>
Ε
κινητική α =
*
Kg *
2 m
2/s
2 =>
Ε
κινητική α =
Joule.
Α3) Υπολογίστε τη μηχανική ενέργεια του αθλητή στο σημείο α.
Ε
μηχανική α = Ε
κινητική α + Ε
δυναμική α =>
Ε
μηχανική α =
Joule +
Joule =>
Ε
μηχανική α =
Joule.
Β1) Υπολογίστε τη δυναμική ενέργεια του αθλητή στο σημείο γ.
Ε
δυναμική γ = m * g * h =>
Ε
δυναμική γ = 50
* 10
/
2 *
m =
.
Β2) Υπολογίστε την κινητική ενέργεια του αθλητή στο σημείο γ.
Επειδή δεν γνωρίζουμε την ταχύτητα στο σημείο γ, αντί να χρησιμοποιήσουμε τον τύπο:
Ε
κινητική γ=0,5*m*v
γ2,
θα χρησιμοποιήσουμε τη διατήρηση της μηχανικής ενέργειας:
Ε
μηχανική γ = Ε
μηχανική α =>
Ε
μηχανική γ =
.
Επίσης,
Ε
μηχανική γ = Ε
κινητική γ + Ε
δυναμική γ =>
= Ε
κινητική γ +
=>
Ε
κινητική γ =
Joule.
Β4) Από τον τύπο της κινητικής ενέργειας υπολογίστε την ταχύτητα του αθλητή στο σημείο γ.
Ε
κινητική γ = 0,5 * μάζα m * ταχύτητα v
γ2 =>
Joule =
* 50
* v
γ2 =>
v
γ2 =
Joule / (
*
Kg) =>
v
γ2 = 2.500 /
m
2/s
2 =>
v
γ2 =
2 m
2/s
2 v
γ =
.
Γ1) Υπολογίστε τη δυναμική ενέργεια του αθλητή στο σημείο δ.
Επειδή τα σημεία α και δ βρίσκονται στο ίδιο ύψος h=5m από το επίπεδο αναφοράς της δυναμικής ενέργειας, έχω:
Ε
δυναμική δ = Ε
δυναμική α =
Γ2) Συμπεράσματα:
1) η κινητική ενέργεια του αθλητή γίνεται μέγιστη στο σημείο
2) η δυναμική ενέργεια του αθλητή γίνεται μέγιστη στα σημεία α και
3) η κινητική ενέργεια του αθλητή μηδενίζεται στα σημεία
και δ
4) η δυναμική ενέργεια του αθλητή μηδενίζεται στο σημείο